О погрешности измерения активности pH/pX

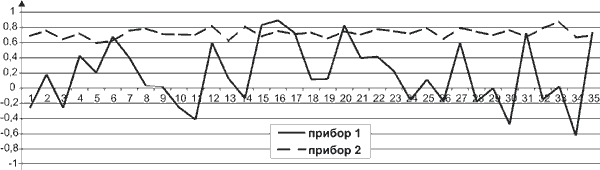
На рис. 1 приведены графики измерения некоторой величины (Е) двумя разными приборами в зависимости от номера измерения.

Рис.1. Измеренные значения в зависимости от номера измерения.

Обратите внимание, что и в первом и во втором случае производитель укажет одну и ту же погрешность - ±1 ед., но в первом случае - это один результат, а во втором - совсем другой. Можно возразить - а в чем собственно, разница, ведь и в первом и во втором случае мы имеем одинаковую точность измерения величины - 1 ед.? Почему это два разных результата, в применении к методу прямой потенциометрии, будет понятно после небольшого отступления.

Значение ЭДС электродной системы и значение pX, (при условии прямой зависимости активности ионов от pX) связывает известное уравнение Нернста:

E=E0+	2,303.R.T	.pX,
	n.F

где:

E₀ - стандартный потенциал электрода, В,
R = 8,314 Дж^.моль^{-1 .}К^-1 - газовая постоянная,
Т - температура, К,
F = 96487 Кл^.моль^-1 - число Фарадея,
n - заряд иона в единицах заряда электрона.

Преобразуем это уравнение к виду:

pX=a(E-E₀),

где коэффициент a учитывает константы и величины, которые можно считать постоянными при данном измерении (n и T).

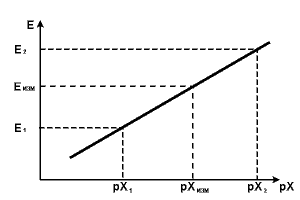
Метод градуировочного графика заключается в определении pX в неизвестном растворе по нескольким (двум) известным.

Здесь E₁ и Е₂, pX₁ и pX₂ - потенциалы электродов в стандартных растворах и соответствующие им значения pX. E_ИЗМ и pX_ИЗМ - измеренное значение потенциала электрода в исследуемом растворе и вычисленное значение pX.

На графике можно наглядно посмотреть влияние погрешности измерения E на вычисление pX по методу градуировочного графика. Для этого нажмите на соответствующую кнопку: Влияние систематической погрешности Влияние случайной погрешности Без учета погрешности измерения

Выведем формулу вычисления pX при известных E₁, E₂, pX₁ и pX₂. Совсем нетрудно увидеть, что:

pXИЗМ=	pX2-pX1	.(EИЗМ-E1)+pX1,
	E2-E1

Теперь вернемся к погрешностям измерения. Запишем измеренные значения потенциала в виде:

E=E_ИСТ+E₀+E_d,

где E_ИСТ - истинное значение, E₀ - систематическая составляющая погрешности, E_d - случайная составляющая.

Если подставить эти значения в предыдущую формулу вычисления pX, то можно убедиться, что систематическая составляющая погрешности измерения потенциала E₀ на погрешность вычисления pX не влияет.

А теперь вернемся к рисунку 1 - графику зависимости измеренной величины от номера измерения. Из графика видно, что у прибора 1 погрешность измерения носит сугубо случайный характер - математическое ожидание близко к нулю (0,182), а среднеквадратическое отклонение (СКО) составляет 0,412. Что касается прибора 2 -здесь погрешность почти систематическая - мат. ожидание 0,723, СКО равно 0,064.

Таким образом, при вычислении pX по методу градуировочного графика первым прибором, погрешность измерения потенциала практически целиком войдет в погрешность вычисления pX, а при вычислении pX вторым прибором погрешность вычисления pX будет в разы (если не на порядок) ниже, чем в первом случае.

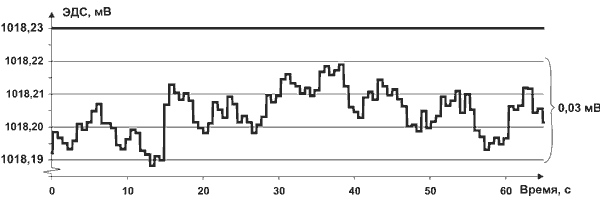
На рис. 2 приведен график зависимости ЭДС, измеренной прибором МУЛЬТИТЕСТ ИПЛ-103, от времени при неизменных условиях измерений. Температура 28,3 °C. Источник эталонной ЭДС - стандартный насыщенный элемент, ГОСТ 5.514-73, класс 0,005, значение ЭДС стандартного элемента - 1018,230 мВ (при указанной температуре), подключенный через имитатор электродной системы И-02, выходное сопротивление имитатора электродной системы - 500 МОм.

Рис.2. Зависимость измеренного значения ЭДС от времени.

Зависимость считана с прибора при помощи ЭВМ, период считывания данных - около 50 мс.

Как видно из представленного графика, систематическая погрешность измерения ЭДС - 0,026 мВ, СКО - 0,007 мВ.

На индикатор прибора выводится округленное значение ЭДС в милливольтах с точностью до одного знака после запятой, и на индикаторе прибора все время измерения выводится величина 1018,2 мВ.

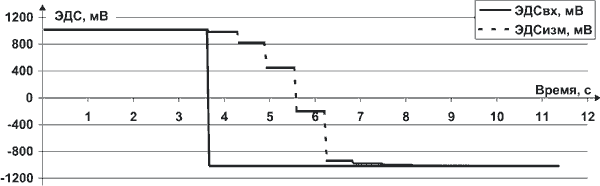
Еще одна особенность pH-метров/иономеров МУЛЬТИТЕСТ - используемые алгоритмы цифровой обработки сигнала позволяют приборам быстро реагировать на изменение входного сигнала, но при этом быть малочувствительными к помехам и наводкам. На рис. 3 приведен график измерения величины ЭДС, при изменении приложенной ЭДС на величину 2036,46 мВ (смены знака приложенной эталонной ЭДС - 1018,23). Условия проведения измерений те же.

Рис.3. Зависимость измеренного значения ЭДС от времени при изменении ЭДС.